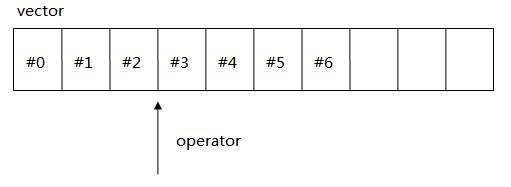
1、快速排序的基本思想:
快速排序排序使用分治的思想,通过一趟排序将待排序列分割成两部分,其中一部分记录的关键字均比另一部分记录的关键字小。之后分别对这两部分记录继续进行排序,递归地以达到整个序列有序的目
2、快速排序的三个步骤:
(1)选择基准:
在待排序列中,按照某种方式挑出一个元素,作为 “基准”
(2)分割操作:
以该基准在序列中的实际位置,把序列分成两个子序列。此时,在基准左边的元素都比该基准小,在基准右边的元素都比基准大
(3)递归地对两个序列进行快速排序,直到序列为空或者只有一个元素。
3、选择基准的方式
一般取序列的第一个或最后一个元素作为基准基本的快速排序
快排的代码实现:
//划分区间排序
template<typename T>
int partition(T arr[], int startindex, int endindex)
{
T key = arr[startindex];
while (startindex < endindex)
{
while (startindex < endindex && arr[endindex] >= key)endindex--;
arr[startindex] = arr[endindex];
while (startindex < endindex && arr[startindex] <= key) startindex++;
arr[endindex] = arr[startindex];
}
arr[startindex] = key;
return startindex;
}
template<typename T>
void Quick(T arr[], int s, int e)
{
//递归算法
if (s < e)
{
int boundindex = partition(arr, s, e);
Quick(arr, s, boundindex - 1);
Quick(arr, boundindex + 1, e);
}
}
template<typename T>
void QuickSort(T arr[], int len)
{
Quick(arr, 0, len - 1);
}
template<typename T>
void Show(T arr[], int len)
{
for (int i = 0; i < len; i++)
{
std::cout << arr[i] << " ";
}
std::cout << std::endl;
}
int main()
{
int arr[30];
for (int i = 0; i < 30; i++)
{
arr[i] = rand() % 1000;
}
int len = sizeof(arr) / sizeof(arr[0]);
Show(arr, len);
std::cout << "---------------------" << std::endl;
QuickSort(arr, len);
Show(arr, len);
return 0;
}
4、快速排序的五种优化
(1)随机取基准点 :
若待排序列是部分有序时,固定选取基准使快排效率底下,取待排序列中任意一个元素作为基准
代码实现:
int arr[30];
for (int i = 0; i < 30; i++)
{
arr[i] = rand() % 1000; //随机取基准值
}
int len = sizeof(arr) / sizeof(arr[0]);
(2)三数取中(优化有序的数据):
对待排序序列中low、mid、high三个位置上数据进行排序,取中间的那个数据作为基准,并用0下标元素存储基准。
代码实现:
template<typename T>
//三数取中
void FindMiddleNumber(T arr[], int left, int mid, int right)
{
if (arr[mid] > arr[right])
{
Swap(arr, mid, right);
}
if (arr[left] > arr[right])
{
Swap(arr, left, right);
}
if (arr[left] < arr[mid])
{
Swap(arr, left, mid);
}
}
(3)小数据的优化 用插入排序 ,最优情况o(n)
对于很小和部分有序的数组,快排不如插排好。当待排序序列的长度分割到一定大小后,继续分割的效率比插入排序要差,此时可以使用插排而不是快排
代码实现:
template<typename T>
//插入排序
void insertSort(T arr[], int startindex, int endindex)
{
int tmp = 0;
int i = startindex + 1;
int j = i - 1;
for (i; i <= endindex; ++i)
{
tmp = arr[i];
for (j = i - 1; j >= startindex && arr[j] > tmp; --j)
{
arr[j + 1] = arr[j];
}
arr[j + 1] = tmp;
}
}
(4)聚集优化
重复数据的优化(数据量大,数值小,离散程度小)
(5)非递归优化
没有开栈,清栈,开销小
代码实现:
//非递归快排
if (s < e)
{
Stack<int> st;
int left = s;
int right = e;
st.push(right);
st.push(left);
while (!st.empty())
{
left = st.top(); st.pop();
right = st.top(); st.pop();
int boundindex = partition(arr, left, right);
//left boundindex - 1 boundindex + 1 right;
if (left < boundindex - 1)
{
st.push(boundindex - 1);
st.push(left);
}
if (boundindex + 1 < right)
{
st.push(right);
st.push(boundindex + 1);
}
}
}
}